#ReadersGarden เล่มที่ 72
คุณได้อะไรจากวิชาคณิตศาสตร์บ้าง? จากตลอด 9 ปีของการศึกษาภาคบังคับ หรือเกือบ 20 ปีหากนับตั้งแต่อนุบาล 1 จนถึงมหาวิทยาลัยปี 4
สำหรับเด็กที่ได้เกรด A วิชาคณิตมาตลอดอย่างซิส หึหึ ตลอดการทำงาน 5 ปี นอกจากคิดเลขง่ายๆ แล้ว ก็ได้ใช้เพียงวิชาสถิติ เช่น หาค่าเฉลี่ย, Max, Min และการทำกราฟแผนภูมินำเสนอข้อมูล ส่วนแคลคูลัส เวกเตอร์ เซต เรขาคณิต ฯลฯ ที่เคยพากเพียรอดหลับอดนอนฝึกทำข้อสอบมานับพันข้อ ทุกวันนี้นอกจากชื่อแล้ว ก็จำอะไรไม่ได้เลยค่ะ 🥲
มานึกๆ แล้ว มันน่าเสียดายเมื่อคิดถึงเวลาเกือบ 20 ปีที่เราตั้งใจเรียนคณิต แต่ตอนนี้กลับรู้สึกเหมือนความจำเสื่อม เพราะที่ผ่านมาเราเพียงแต่ท่องจำสูตรไปเพื่อสอบให้ผ่าน แต่ไม่ได้เข้าใจเลยว่าเราเรียนคณิตไปทำไม นำมาใช้ประโยชน์ได้อย่างไรบ้าง เราจำเป็นต้องเรียนครอบคลุมทุกศาสตร์ขนาดนั้นเลยหรือ
หากเพื่อนๆ สงสัยเหมือนกัน หนังสือภาษาจักรวาลเล่มนี้มีคำตอบ! เขียนโดยคุณอาจวรงค์ จันทมาศ นักสื่อสารวิทยาศาสตร์ที่อธิบายเรื่องยากๆ อย่างวิทย์และคณิตให้คนทั่วไปอย่างพวกเราเข้าใจง่ายขึ้นและรู้สึกสนุกขึ้น
หนังสือเล่มนี้เล่าประวัติศาสตร์สนุกๆ ฉบับย่อของคณิตศาสตร์ที่พวกเราคุ้นชื่อกันดี เช่น เรขาคณิค ภาคตัดกรวย แคลคูลัส ความน่าจะเป็น การย้ายข้างสมการ เป็นต้น ว่าศาสตร์เหล่านี้มีที่มาอย่างไร ใครเป็นผู้คิดค้น คิดค้นขึ้นมาทำไม และนำไปใช้ประโยชน์อย่างไร
ขอสรุปประเด็นหลักที่ได้จากหนังสือ 4 ประเด็นดังนี้ค่ะ
คณิตศาสตร์กับการใช้งาน เรียนไปทำไม?
ในชีวิตประจำวันของพวกเรา คณิตศาสตร์ที่ถูกนำมาใช้บ่อยๆ คงจะเป็นการคิดเลข คำนวณรายรับ-รายจ่าย คำนวณเปอร์เซ็นต์ส่วนลดเวลาซื้อของ หรือความน่าจะเป็นที่จะสุ่มได้คาแรกเตอร์โปรดเวลาสุ่มกาชา ซึ่งนั่นเป็นเพียงเศษเสี้ยวเล็กๆ ของบทเรียนในวิชาคณิตที่พวกเราเรียนกันมา มาดูกันว่าแล้วบทเรียนอื่นๆ ถูกนำมาใช้งานจริงอย่างไรบ้าง

เริ่มต้นกันที่ แคลคูลัส วิชาบังคับที่นิสิตปี 1 คณะวิทยาศาสตร์ต้องเรียนกันทุกคน คนที่เรียนภาควิชา Geology อย่างซิสก็เช่นกัน ซึ่งหลังจากสอบผ่านแล้วก็ไม่ได้ยินชื่อวิชานี้อีกเลย และไม่เคยรู้ว่าสรุปแล้ว f'(x) = dy/dx (x≠0) เอาไปใช้ทำอะไร!?
คุณอาจวรงค์เล่าว่า แคลคูลัสว่าด้วยเรื่องการคำนวณหา ‘ความชัน’ และ ‘พื้นที่ใต้กราฟ’ ให้ลองนึกถึงสะพานข้ามแม่น้ำที่มีลักษณะโค้ง หากวางลูกบอลไว้กลางสะพานซึ่งเป็นตำแหน่งสูงสุด ลูกบอลจะไม่กลิ้งไปไหนเพราะไม่มีความชัน แต่หากขยับลูกบอลไปจุดอื่นๆ ของสะพาน ลูกบอลจะกลิ้งเพราะความชันไม่เท่ากับศูนย์ ซึ่งเราสามารถใช้แคลคูลัสคำนวณหาความชันของแต่ละจุดและพื้นที่ใต้สะพานได้
ดังนั้นประโยชน์ของแคลคูลัสคือ ช่วยวิเคราะห์ธรรมชาติของเส้นโค้งได้อย่างลึกซึ้งและสะดวก ทำให้วิศวกรออกแบบโครงสร้างได้หลากหลาย นักเศรษฐศาสตร์วิเคราะห์แนวโน้มและปริมาณทางการเงินได้ และนักฟิสิกส์หาตำแหน่งและความเร็วของสิ่งที่ต้องการได้
ส่วนวิชาเรขาคณิตที่ว่าด้วยเรื่องของรูปร่าง รูปทรง ขนาดและตำแหน่งของวัตถุ ที่พวกเราคุ้นเคยกับการท่องสูตรหาพื้นที่รูปและเส้นรอบรูปของสี่เหลี่ยม สามเหลี่ยม วงกลม วงรี ฯลฯ เรขาคณิตถูกนำมาใช้ออกแบบสิ่งต่างๆ รวมถึงเครื่องมือทางการแพทย์ที่เรียกว่า Lithotripter ซึ่งเป็นเครื่องมือสลายนิ่วด้วยคลื่นกระแทก โดยใช้ประโยชน์จากคุณสมบัติการสะท้อนของวงรี

วงรีมีจุดโฟกัสอยู่ 2 จุด หากมีลำแสงพุ่งจากจุดโฟกัสด้านหนึ่ง ไม่ว่ามันจะพุ่งไปทิศทางไหน สุดท้ายแล้วมันจะสะท้อนกลับมาที่จุดโฟกัสอีกจุดเสมอ คุณอาจวงค์ยกตัวอย่างให้เห็นภาพไว้ว่า “หากฉาบกระจกไว้ในผนังรูปวงรี แล้วนำหลอดไฟไปเปิดไว้ที่จุดโฟกัสด้านหนึ่ง แสงจากหลอดไฟไม่ว่าจะพุ่งทุกทิศทางแล้วไปตกกระทบที่กระจกจากนั้นจะสะท้อนไปยังจุดโฟกัสอีกจุดของวงรีเสมอ”
หลักการเรียบง่ายนี้ถูกใช้ในเครื่อง Lithotripter โดยการปล่อยคลื่นอัลตราซาวน์ที่จุดโฟกัสหนึ่งของวงรีไปรวมกันที่จุดโฟกัสอีกจุดเพื่อสลายนิ่ว ช่วยให้สลายก้อนนิ่วขนาดเล็กได้โดยไม่ต้องผ่าตัด
นอกจากแคลคูลัสและเรขาคณิตแล้ว ยังมีการใช้ทฤษฎีกราฟในการวางแผนขนสินค้า หรือประยุกต์ใช้กับโลกออนไลน์อย่างระบบ PageRank Algorithm ที่ Google ใช้จัดลำดับการแสดงผลเว็บไซต์เวลาค้นหา และการนำบทเรียนทางคณิตมาประยุกต์ใช้จริงอีกมากมาย
คณิตศาสตร์กับธรรมชาติ มีอยู่หรือสร้างขึ้น?
คำถามหนึ่งที่น่าสนใจจากหนังสือคือ “คณิตศาสตร์เป็นสิ่งที่มีอยู่ตามธรรมชาติ หรือเป็นสิ่งที่มนุษย์สร้างขึ้น?”

เราเห็นแล้วว่าคณิตศาสตร์แฝงอยู่ในธรรมชาติ เช่น เส้นโค้งของภาคตัดกรวยมีลักษณะเหมือนกับวงโคจรภายใต้กฏแรงโน้มถ่วงของดวงอาทิตย์ โดยโคจรเป็นเส้นโค้ง 4 แบบ ได้แก่ วงกลม วงรี พาราโบรา และไฮเปอร์โบลา
เกลียวก้นหอยก็สามารถพบเจอในธรรมชาติ เช่น ยอดอ่อนของต้นเฟิร์น งวงดูดน้ำหวานของผีเสื้อ สนามแม่เหล็กที่ดวงอาทิตย์แพร่ออกมา และกาแล็กซีบางประเภท
แต่ทว่าคณิตศาสตร์มีอยู่ในธรรมชาติเหล่านี้อยู่แล้ว แล้วมนุษย์ไปค้นพบเข้า หรือว่าคณิตศาสตร์เป็นสิ่งที่มนุษย์คิดค้นขึ้นมาเองเพื่ออธิบายสิ่งต่างๆ ในธรรมชาติ
เรื่องนี้ทำให้ซิสนึกถึงเรื่องเล่าของลัทธิพิธากอรัส (Pythagoreanism) ซึ่งได้ยินครั้งแรกจากรายการลึกลับครับผม ตอน ลัทธิพิศดาร เราอาจจะคุ้นเคยกับชื่อพิธากอรัส (Pythagoras) ตอนสมัยม.ต้น จากสูตรหาความยาวด้านของสามเหลี่ยมมุมฉาก a2= b2 + c2 ซึ่งพิธากอรัสเป็นผู้คิดค้นทฤษฎีบทนี้และยังถูกยกย่องว่าเป็นบิดาแห่งตัวเลขด้วย
สำหรับลัทธิพิธากอรัส บรรดาสาวกซึ่งเป็นลูกศิษย์ของพิธากอรัสมีความเชื่อว่าคณิตศาสตร์เป็นรากฐานของจักรวาล เอกภพมีระเบียบและความกลมกลืนกันซึ่งถูกควบคุมโดยหลักการทางคณิตศาสตร์ ทุกสิ่งทุกอย่างถูกสร้างขึ้นและอธิบายได้ด้วยตัวเลข ดังนั้นตัวเลขเป็นองค์ประกอบสำคัญของจักรวาลและเป็นตัวแทนของแนวคิด ซึ่งตอนที่ซิสได้ฟังหลักการคิดของลัทธินี้ ก็รู้สึกถูกโน้มน้าวตามและเชื่อว่าคณิตศาสตร์แฝงอยู่ในธรรมชาติอยู่แล้วจริงๆ แต่ก็เชื่อว่าบางเรื่องในคณิตศาสตร์ก็เป็นสิ่งที่มนุษย์คิดขึ้นมาเพื่ออธิบายธรรมชาติ
คณิตศาสตร์กับศิลปะ ความงดงามของรูปแบบ
หนังสือเล่มนี้ยังแสดงให้เห็นถึงความงดงามของโลกคณิตศาสตร์ที่เกิดจากรูปแบบต่างๆ เช่น ก้นหอยของอูแลม (Ulam Spiral) ที่เกิดจากจำนวนเฉพาะ หมายถึงตัวเลขที่มีเฉพาะตัวมันเองและเลข 1 หารลงตัว เช่น 2, 3, 5, 7, 11, 13, 17, 19 เป็นต้น (อีกหนึ่งความอัดอั้นตันใจ สมัยประถมโดยบังคับให้ท่องจำนวนเฉพาะไปจนถึง 97 ตอนนี้ก็ยังจำเลขได้และงงว่าจำทำเพื่อ!? 😂)
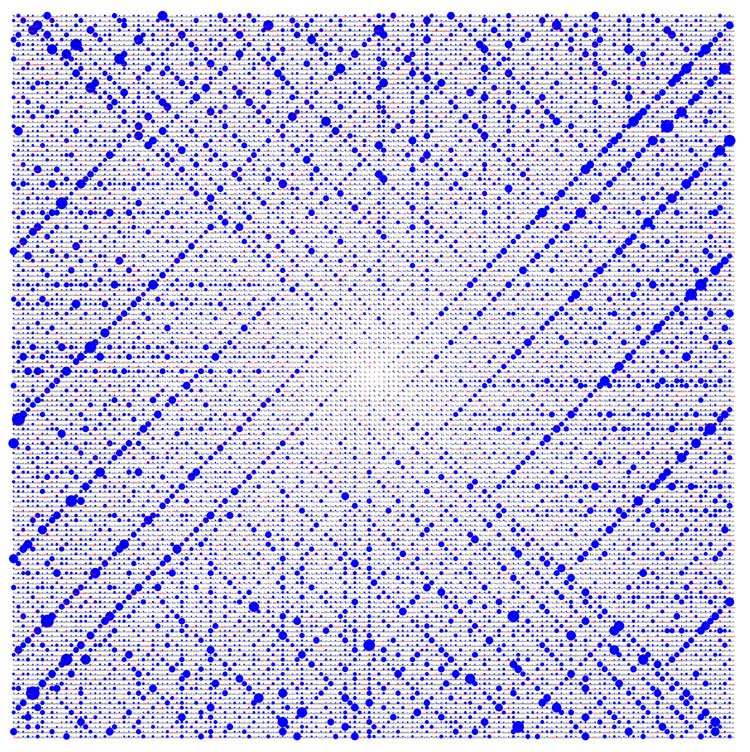
ก้นหอยของอูแลมเป็นรูปแบบที่เกิดจากการเขียนจำนวนเต็มเริ่มจากเลข 1 อยู่ตรงศูนย์กลาง เพิ่มจำนวนไปเรื่อยๆ เป็นชั้นๆ เมื่อตัดเลขให้เหลือแต่จำนวนเฉพาะ พบว่าจำนวนเฉพาะปรากฏหนาแน่นในแนวทแยง ซึ่งดูมีรูปแบบมากกว่าจะเป็นการกระจายแบบสุ่ม แต่ยังหาเหตุผลอธิบายลึกซึ้งไม่ได้ แม้จะยังไม่ทราบเหตุผลแน่ชัด แต่ลวดลายของก้นหอยอูแลมเป็นรูปแบบจากตัวเลขงดงามและน่าทึ่ง
นอกจากนี้ยังมีเกลียวก้นหอยของธีโอโดรัส (Spiral of Theodorus) เป็นก้นหอยที่เกิดจากการนำสามเหลี่ยมมุมฉากมาต่อกัน
ในวงการศิลปะก็นำหลักการทางคณิตศาสตร์มาสร้างสรรค์ผลงานเช่นกัน หนึ่งในนั้นเป็นงานของศิลปินชื่อดัง เอ็ม.ซี.แอ็ชเชอร์ (M.C.Escher) ผู้ใช้คณิตและฟิสิกส์เป็นแรงบันดาลใจในงานศิลปะ เช่น ภาพ Reptile (1943) และ Sky and Water I (1938) ที่ใช้หลักการเรขาคณิต Tessellation คือการปูกระเบื้องระนาบเรียงต่อกันโดยไม่มีช่องว่าง ซึ่งตามรูปเรขาคณิตทั่วไปแล้ว ใช้ได้กับสี่เหลี่ยม หกเหลี่ยม สามเหลี่ยม แต่แอ็ชเชอร์นำมาใช้กับการวาดรูปสิ่งมีชีวิต



นอกจากนี้ยังมีภาพ Waterfall (1961) ที่เล่นกับมุมมองสายตา (Perspective) หากสังเกตขอบรางน้ำ ตอนแรกน้ำไหลลงมาสู่ด้านล่าง แต่เมื่อมองไล่ตามรางน้ำไปเรื่อยๆ จะพบว่าน้ำไหลกลับไปอยู่จุดบนสุด หากมีน้ำตกลักษณะนี้จริง จะสามารถสร้างพลังงานได้อย่างไม่มีที่สิ้นสุด แม้ในความเป็นจริงจะทำไม่ได้เพราะผิดกฏฟิสิกส์
คณิตศาสตร์กับความหลงใหล
คณิตศาสตร์บางเรื่องก็ไม่ได้ถูกนำมาประยุกต์ใช้อย่างชัดเจน ไม่ได้ใช้อธิบายธรรมชาติ หรือไม่ได้อยู่ในงานศิลปะ แต่ก็ยังมีคนบางกลุ่มที่หลงใหลในคณิตศาสตร์จนเป็นงานอดิเรก
เช่น ค่าพาย (π) เราอาจคุ้นเคยกันว่าค่าพายใช้หาเส้นรอบวงกลมจากสูตร 2πr และหาพื้นที่วงกลมจากสูตร πr² โดยท่องจำกันมาว่าค่าพายเท่ากับ 22/7 หรือ 3.14 ซึ่งเป็นจำนวนอตรรยะที่มีทศนิยมไม่ซ้ำกันไม่รู้จบ
บางคนสนใจถึงขนาดใช้เวลาทั้งชีวิตในการหาค่าพาย เมื่อสองร้อยกว่าปีก่อน คุณครูชาวอังกฤษคนหนึ่งมีงานอดิเรกคือหาค่าพาย เขาคือวิลเลียม แชงก์ส (William Shanks) โดยใช้เวลาว่างหาค่าพายไปจนถึงทศนิยมตำแหน่งที่ 707 แม้ว่าจะมีการพิสูจน์ภายหลังด้วยเครื่องคอมพิวเตอร์ว่าเขาคำนวณถูกถึงตำแหน่งที่ 527 เท่านั้น แต่ก็ยังน่าทึ่งอยู่ดี
การคำนวณหาค่าพายว่ายากแล้ว ท่องจำค่าพายยิ่งยากกว่า! ราชเวียร์ มีนา (Rajveer Meena) นักศึกษาหนุ่มชาวอินเดียถูกบันทึกว่าเป็นผู้สร้างสถิติโลกด้วยการใช้เวลา 9 ชั่วโมง 27 นาที ท่องค่าพายไปได้ 70,000 ตำแหน่ง!! แต่ส่วนสถิติแบบไม่เป็นทางการตกเป็นของคุณอากิระ ฮะระกูชิ (Akira Haraguchi) วิศวกรวัยเกษียณที่ท่องค่าพายได้ถึง 100,000 ตำแหน่ง!!!
ในฐานะคนที่จำตัวเลข 10-13 หลักของบัญชีธนาคารหรือบัตรประชาชนตัวเองยังผิดๆ ถูกๆ รู้สึกทึ่งมาก 😮👏 แน่นอนว่าย่อมเกิดคำถามในหัวว่า “ทำไปทำไม!?” ทั้งที่ใช้ค่าพาย = 3.14 ก็เพียงพอแล้ว แต่เมื่อนึกถึงงานอดิเรกของเราเองที่ทำเพียงเพราะว่า “มันสนุกดี” ไม่ได้ทำเพื่อหวังผลประโยชน์ใดๆ ก็พอจะเข้าใจความรู้สึกของพวกเขาขึ้นมาบ้าง เหตุผลเหมือนกับที่คุณอาจวงค์กล่าวไว้ว่า
“ความสวยงามของสมการ Euler’s Identity (สมการที่งดงามที่สุดในโลกคณิตศาสตร์) ผลรวมเศษส่วนของ Basel Problem จนถึง Euler Line นั้นอาจไม่ได้มีการประยุกต์ใช้ที่ชัดเจน แต่ความงามเหล่านี้ก็ไม่ต่างอะไรจากดอกไม้ อัญมณี หรือแม้แต่ทิวทัศน์ที่ไม่ได้ช่วยให้เราอิ่มท้อง แต่ช่วยให้เราอิ่มเอม”
– อาจวรงค์ จันทมาศ, หนังสือภาษาจักรวาล
ซื้อหนังสือ: นายอินทร์, SE-ED, Kinokuniya